Question 1
The volume of a cone can be determined by summing up the infinitesimal circular cross-sections of the cone across the length of the cone Consider the function f(x) = x2 for x contained in [0,1].
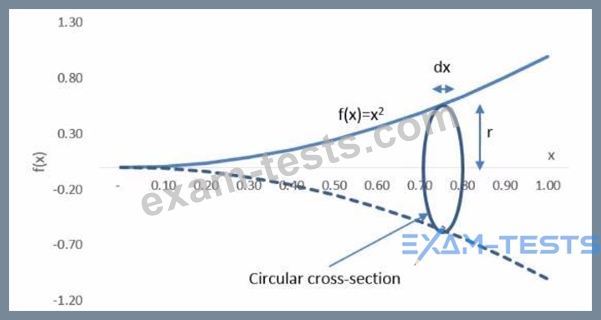
Now consider an infinitesimal circular cross-sectional element of width dx and radius r = f(x) Determine the volume of the cone enclosedby the function f(x) by considering the volume of each circular cross-sectional element (Recall thatthe sum of infinitesimal elements can be represented as an integral Recall also that the area of a
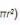
circle is
A)
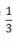
B)
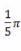
C)
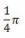
D)
1

Now consider an infinitesimal circular cross-sectional element of width dx and radius r = f(x) Determine the volume of the cone enclosedby the function f(x) by considering the volume of each circular cross-sectional element (Recall thatthe sum of infinitesimal elements can be represented as an integral Recall also that the area of a
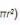
circle is
A)
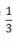
B)
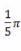
C)
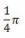
D)
1
Question 2
Let X be a continuous random variable with probability density function f(x) that is defined over all real numbers.
DefineE[g(X)]whereg(x)is a continuous function.
A)
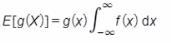
B)
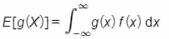
C)
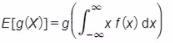
D)
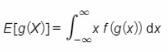
DefineE[g(X)]whereg(x)is a continuous function.
A)
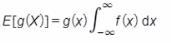
B)
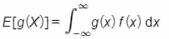
C)
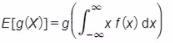
D)
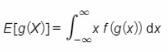
Question 3
Identify which of the following statements is true,where X is a discrete random variable that exists over the domain [a. b], and F(x) is its distribution function.
A)
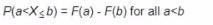
B)
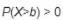
C)

D)
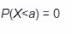
A)
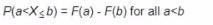
B)
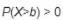
C)

D)
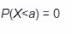
Question 4
Consider the three vectors:
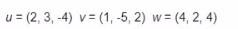
Determine which of (he vectors or combination of vectors shown in the options has the greatest magnitude
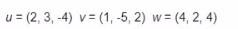
Determine which of (he vectors or combination of vectors shown in the options has the greatest magnitude
Question 5
Identify which of the following statements are true.
I.Skewness measures how peaked a set of data is
II.Skewness is a measure of asymmetry of the distribution of the data about its mean.
III. For a symmetrically distributed data, the mean equals the median but not necessarily the mode IV. The value of a measure of skewness can be positive, zero or negative.
I.Skewness measures how peaked a set of data is
II.Skewness is a measure of asymmetry of the distribution of the data about its mean.
III. For a symmetrically distributed data, the mean equals the median but not necessarily the mode IV. The value of a measure of skewness can be positive, zero or negative.

